Настоящая работа посвящена исследованию пространственных сверхзвуковых струй, истекающих из сопел нетрадиционной формы (прямоугольных, треугольных, многолепестковых). Число работ, посвященных исследованию такого рода струйных течений, крайне ограничено, хотя применение "необычных" струй представляется перспективным с точки зрения интенсификации различных технологических процессов путем активного управления структурой потока за выходным сечением сопла, снижения интенсивности излучения струй ракетных и авиационных двигателей в акустическом, тепловом и других диапазонах.
При проведении исследований использован оригинальный метод расчета на основе модифицированной схемы Иванова-Крайко с адаптирующейся к линиям тока расчетной сеткой. При этом обеспечивается экономичность расчета, построение расчетной сетки для областей произвольной конфигурации, автоматическое сгущение и, следовательно, повышение точности расчета в областях с резким изменением параметров типа скачков уплотнения. Применение метода не требует наличия какой-либо априорной информации об очертаниях расчетной области. Некоторые результаты проведенных расчетов приведены ниже.
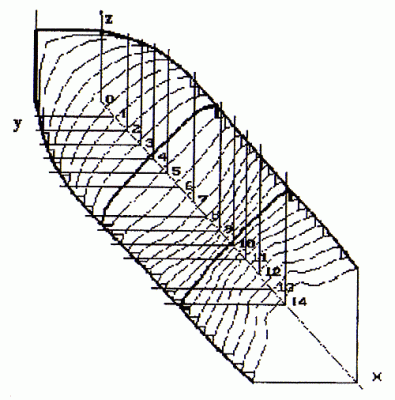
При исследовании струй, истекающих из сопел прямоугольной и квадратной формы, в первую очередь, обращает на себя внимание эффект неравномерного расширения потока в поперечном направлении.
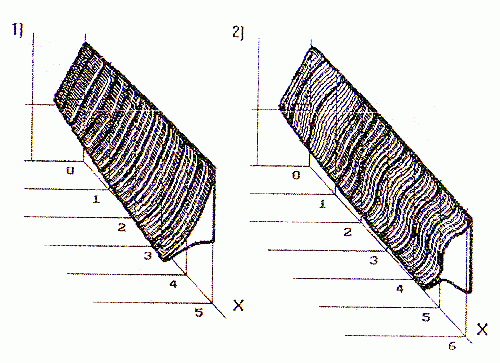
Так, на рис.1 показаны внешние очертания струи, истекающей из квадратного сопла с параметрами на срезе: n=2, Мa=3, поток параллелен оси ОХ. Необходимо отметить различие в характере изменения параметров в плоскости ХОY и "диагональной" плоскости, т.е. плоскости, проходящей через ось OX под углом 45° к плоскости XOY. На одинаковом удалении от выходного сечения процессы расширения-сжатия происходят гораздо интенсивнее в направлении диагональной плоскости. Анализ распределения давления в поперечных сечениях доказывает образование ярко выраженной зоны разрежения в направлении диагонали, что в дальнейшем приводит к образованию в том же направлении сильной ударно-волновой структуры. В результате на некотором расстоянии от среза сопла граница струи и висячий скачок приобретают в поперечном сечении ромбовидную форму, развернутую относительно проекции кромки сопла на 45°.
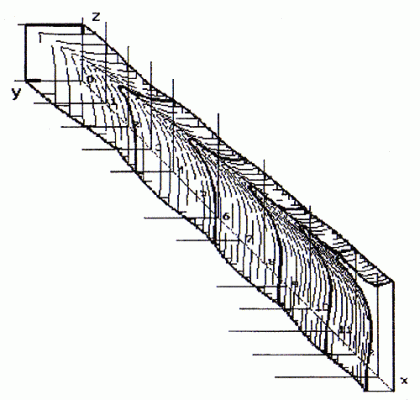
Еще более интересные результаты были получены при исследовании квадратных перерасширенных струй с неравномерным распределением параметров в выходном сечении сопла.
На рис.2 приведены очертания такой струи со следующими параметрами на срезе: Мa=2 и n=0.9, угол полураствора сопла в вертикальной плоскости - 10°, в горизонтальной - 0° (рассчитывалась одна из четвертей струи). В этом случае имеет место значительно более сильная деформация потока за срезом сопла - можно отметить наличие углового выступа, сильное расширение в вертикальной плоскости симметрии и одновременное сжатие в горизонтальной. Причем, несмотря на наличие четко выраженной периодической структуры в плоскостях XOY и XOZ, величина углового выступа практически не изменяется. Геометрический фактор - угол полураствора сопла, который не оказывает заметного влияния на формирование осесимметричной струи, в данном случае играет ключевую роль и в значительной степени определяет характер течения.
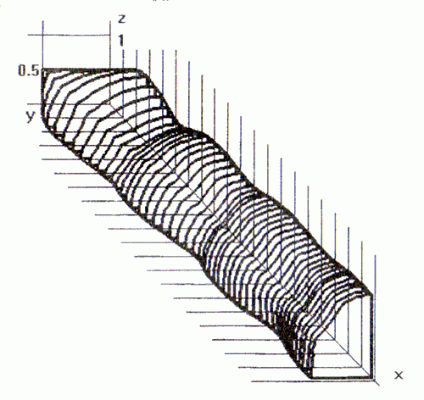
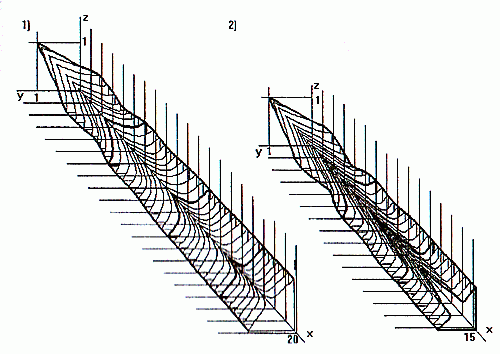
Предлагаемым методом проведены расчеты полностью прямоугольного сопла с отношением сторон в выходном сечении 1:2 (длина половины большой стороны принята равной 1) . Параметры на срезе Ма=2, n=2.
Увеличение размеров струи происходит в направлении оси OZ ( рис.3). Одновременно струя сжимается в плоскости симметрии сопла, параллельной его большой стороне. Происходит постепенный "поворот" струи вдоль собственной оси примерно на 45° (поэтому граница струи в поперечном сечении принимает ромбовидную форму) . Наибольшая интенсивность ударно-волновых процессов отмечается в направлении самых близких (к оси симметрии струи) точек границы среза сопла. Аналогичные результаты дает расчет струи, истекающей из прямоугольного сопла с отношением сторон 1:3 и 1:5. Данный эффект имел место только на режиме недорасширения. При небольших значениях угла полураствора сопла в вертикальной плоскости (порядка 5-10°) эта особенность наблюдается более отчетливо.
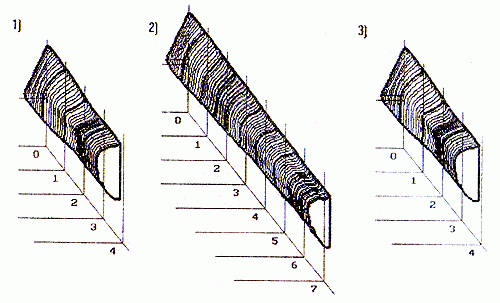
Применение струй, истекающих из треугольных сопел, представляется весьма перспективным направлением развития ряда технологических процессов. При этом даже незначительная неравномерность распределения параметров на срезе сопла приводит к формированию качественно отличающихся струйных потоков. При относительно равномерном распределении параметров на срезе сопла недорасширенные струи имеют следующую ярко выраженную особенность.
На расстоянии порядка 3-5 характерных размеров струя приобретает в поперечном сечении форму треугольника, перевернутого на 180° ( рис.4), что оказывает принципиальное влияние на ударно-волновую структуру струи (и, например, на характер взаимодействия с преградой). Струя в большей степени расширяется в направлении самых близких (к оси симметрии струи) точек границы среза сопла. Главным параметром, усиливающим эффект неравномерного расширения, является значение нерасчетности (в случае недорасширенных струй). Для перерасширенных струй подобный эффект не наблюдался.
В том случае, если на срезе сопла реализуется неравномерное распределение (например, по типу "течения от источника"), ударно-волновая структура струи и ее очертания приобретают абсолютно иную форму ( рис.5).
Аналогичное явление отмечалось и при расчете струй, истекающих из сопл с выходным сечением в форме правильного шестиугольника и восьмиугольника. Распределения относительного статического давления на оси струи, истекающей из сопел с квадратным, шестиугольным и восьмиугольным срезом практически совпадает.
Расчет струи, истекающей из звездообразного сопла, показывает, что форма выходного сечения сопла и неравномерность параметров на его срезе может привести к качественному изменению структуры потока. Отклонение вектора скорости потока от оси ОХ в выходном сечении сопла вызывает, например, увеличение площади поверхности струи.
На рис.6 показаны очертания внешней границы струи, истекающей из сопла с параметрами на срезе: Ma=2, n=1.5. В первом случае поток параллелен оси ОХ, во втором случае реализовано "течение от источника". Максимальное значение угла отклонения вектора скорости от оси ОХ составляет 3°. Как и следовало ожидать, процессы расширения-сжатия в плоскости симметрии луча звезды проходят во втором случае более интенсивно, при этом лучевой выступ практически не меняет размеров. В первом случае струя принимает почти ромбовидные (в поперечном сечении) очертания.
Использование особенностей струйных потоков, истекающих из сопл нетрадиционной формы позволяет удовлетворить разнообразные требования, возникающие при проектировании технологических процессов.
Применение струй, истекающих из треугольного в выходном сечении сопла, позволяет увеличить силовое воздействие на преграду при правильном взаимном расположении сопла и преграды (т.е. при определенной ориентации выходного сечения сопла и расстоянии до преграды).
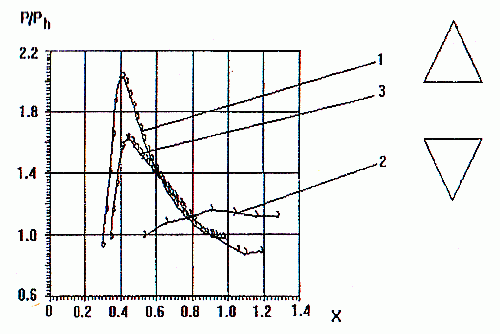
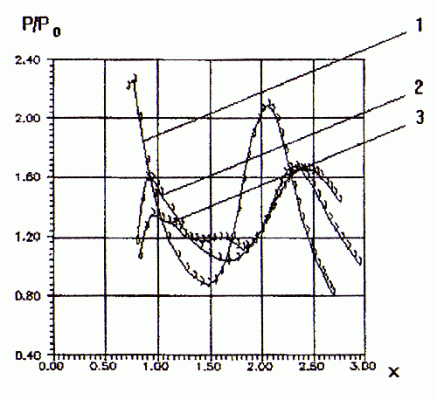
В случае применения треугольного сопла, сориентированного вершиной вверх ( рис.7), наблюдается значительное превышение относительного статического давления за первой ударной волной на преграде (в сравнении с воздействием струи, истекающей из эквивалентного осесимметричного сопла).
К аналогичному результату приводит использование струй, истекающих из прямоугольных сопл ( рис.8). При горизонтальной ориентации сопла (когда большая сторона его выходного сечения параллельна горизонтальной оси ОY) достигается значительное увеличение силового воздействия на преграду как в первой ударной волне, так и во второй.
Основным газодинамическим параметром, влияющим на интенсивность ударно-волновой структуры в струе и на преграде является значение нерасчетности. В то же время неравномерность распределения параметров на срезе сопла может привести к качественным изменениям структуры струи, что вызывает необходимость проводить расчет с конкретным набором параметров. Поэтому представляется невозможным сформулировать общие рекомендации по вопросу о том, какой формы сопла должны применяться. Можно однозначно утверждать, что использование сопла с выходным сечением неосесимметричной формы позволяет добиваться значительного увеличения или уменьшения силового воздействия на преграду.